Machine learning#
Supervised learning#
입력벡터 \(x\in\R^d\)와 출력값 \(y\in\R\)가 대략적으로 아래와 같은 관계를 갖는다고 하자.
입력벡터 \(x\)를 independent variable 또는 feature vector 라고 부른다.
출력값 \(y\)는 outcome, response, target, label, 또는 dependent variable 이라 부른다. 보통 \(y\)가 머신러닝 모델을 통해 예측하고자 하는 값이 된다.
실제로는 \(x\)와 \(y\) 사이의 정확한 관계는 알 수 없는 경우가 대부분이다.
Features#
머신러닝 모델의 입력 벡터 \(x\)는 입력 데이타의 특징들을 수치화한 벡터이다.:
문서 데이타:
문서의 경우, 정해진 사전에 포함된 단어들 각각에 대해 해당 문서에 나타나는 빈도를 수치화한 word count histogram 을 feature vector로 사용할 수 있다.
환자 데이타:
환자의 개인정보 및 검사결과 등을 수치화하여 feature vector로 사용할 수 있다.
고객 데이타:
고객 각각의 물품 구매이력과 고객의 개인정보 등을 수치화하여 feature vector로 활용할 수 있다.
Where features come from#
이미지, 비디오, 오디오, 문서 등, 입력에 사용되는 실제 데이타(수치화되지 않았을 수도 있음)를 \(u\)라고 부르자.
실제 데이타와 피처 벡터는 \(x = \phi(u)\)와 같은 관계로 정의하며, 이 함수 \(\phi\)를 embedding 또는 feature function 이라 한다.
임베딩 함수 \(\phi\)는 단순할 수도 있으며 매우 복잡할 수도 있다.
마찬가지로 출력에 대해서도 수치화되지 않은 실제 데이타 \(v\)와 모델 출력값 \(y\)의 관계를 \(y=\psi(v)\)와 같은 임베딩 함수로 표현한다.
Data and prior knowledge#
짝지어진 \(n\)쌍의 데이타 세트를 \(x^{(t)},\dots,x^{(n)} \in \R^d\)와 \(y^{(1)},\dots,y^{(n)} \in \R\)로 표현하자.
\((x^{(i)},y^{(i)})\)는 \(i\)번째 data pair , observation , example 라고 할 수 있다.
데이타 또는 데이타간의 관계에 대한 사전 정보(prior knowledge)가 활용될 수도 있다. 예를 들어 관계 함수 \(f\)가 연속적인 함수인지, 또는 출력 \(y\)가 항상 양수인지 등의 사전정보를 활용하면 머신러닝 예측 성능을 개선할 수도 있다.
Predictor#
예측기(predictor) 또는 모델(model)을 \(g:\R^d \rightarrow \R\)와 같이 정의한다.
예측기는 피처 벡터 \(x\)로부터 출력 \(y\)를 예측해내는 역할을 하며, 예측기의 출력값을 \(\hat{y}\)로 표현한다. 즉, \(\hat{y} = g(x)\)로 표현한다.
주어진 데이타와 사전지식을 활용하여 예측기 \(g\)가 주어진 데이타를 잘 설명하도록 \(g\)를 정하는 일을 머신러닝 모델을 학습한다고 한다.
수치화되지 않았던 날것의 데이타들로는 아래와 같은 관계로 설명할 수 있다.
예측치 \(\hat y^{(i)}\)와 실제 출력값 \(y^{(i)}\)가 가깝다면, 즉 \(\hat y^{(i)} \approx y^{(i)}\)라면, 예측기가 \(i\)번째 데이타를 잘 설명한다고 할 수 있다.
그러나 실제로 머신러닝 문제의 목표는 학습 과정에서 보지 못했던 데이타에 대해서도 \(\hat y \approx y\)를 잘 만족하도록 하는 모델을 설계하는 것이다.

Information flow#

Linear predictor#
아래와 같이 피처 벡터 \(x\)에 대한 선형함수로 표현되는 선형 예측기가 널리 사용된다.
여기서 벡터 \(\theta\in \R^d\)는 예측기를 표현하는 파라미터로, predictor parameter vector 라고 한다.
이와 같은 모델을 regression model 이라고도 부른다.
\(x_j\)는 \(j\)번째 피처 성분을 믜미하며, 예측기의 출력값은 피처들의 선형 조합으로 표현된다.
이제, 예측기 설계 문제는 주어진 데이타를 가장 잘 설명하는 예측기 파라미터 벡터 \(\theta \in \R^d\)를 고르는 문제가 된다.
예측기가 \(\theta\)로 설명되므로, \(g_\theta(x)\)로 표현하기도 한다.
Interpreting a linear predictor#
예를 들어, \(\theta_3\)는 세 번째 피처 \(x_3\)의 증가에 따라 예측값 \(\hat y = g(x)\)가 증가하는 비율로 이해할 수 있다.
예를 들어, \(\theta_7=0\)은 일곱번째 피처가 예측값에 아무런 영향을 주지 못한다는 의미가 된다.
\(\theta\)의 크기가 작다는 것은 예측기가 \(x\)의 변화에 민감하지 않다는 뜻이 된다:
Affine predictor#
만약 우리가 첫번째 피처 \(x_1\)을 상수 1로 지정했다고 하면, 선형 예측기는 나머지 피처 \(x_{2:d}\)에 대한 affine function 이 된다.
이 때, 첫번째 파라미터 \(\theta_1\)를 예측기의 offset 또는 constant term 이라고 부른다. 이 파라미터는 나머지 모든 피처가 0일 때의 예측값을 의미하기도 한다.
Empirical risk minimization#
Loss function#
예측 모델의 정확도를 표현하기 위해, 다음과 같이 loss function 또는 risk function, \(\loss:\R \times \R \to \R\) 정의하여 \(\hat y\)와 \(y\)의 차이를 정량화한다.
여기서 \(\loss(\hat y, y)\)는 예측값 \(\hat y\)가 얼마나 실제 출력값 \(y\)와 가까운지를 표현한다.
통상적으로 모든 \(\hat y\), \(y\)에 대해 \(\loss(y,y)=0\) 이며\(\loss(\hat y,y)\geq 0\)이다.
Examples
quadratic loss:
absolute loss:
fractional error: for \(\hat y, y >0\),
(100을 곱해 퍼센트 오차로 표현하기도 한다.)
Empirical risk#
예측기 \(g\)가 모든 데이타 \((x^{(i)},y^{(i)})\), \(i=1, \ldots, n\)에 대해 좋은 성능을 갖는 것이 바람직하므로, 아래와 같이 모든 데이타들에 대한 평균 loss 값으로 정의되는 empirical risk 를 정의한다.
만약 \(\eloss\)가 작다면 주어진 데이타 세트에 대해 예측기의 성능이 좋다고 할 수 있다.
예측기가 파라미터 \(\theta\)로 표현되는 경우, 아래와 같이 구체적으로 표현할 수 있다.
Mean square error#
제곱 함수로 표현되는 손실함수 \(\loss (\hat y, y) = (\hat y-y)^2\)가 적용되는 경우, empirical risk는 mean-square error (MSE)가 된다.
이 값에 제곱근을 취해 root-mean-square error, \(\text{RMSE} = \sqrt{\text{MSE}}\), 출력 \(y^{(i)}\)와 같은 단위를 갖는 값으로 예측기 평균 오차를 표현하기도 한다.
Mean absolute error#
절댓값으로 표현되는 손실함수 \(\loss (\hat y, y) = |\hat y-y|\)가 적용되면, empirical risk는 mean-absolute error 가 된다.
이 경우는 이 자체가 출력 \(y^i\)와 동일한 단위를 갖는다.
이는 위에서 정의한 mean-square error와 유사해 보이지만 많은 면에서 그렇지 않다.
Empirical risk minimization#
how do we pick our prediction rule \(g\)?
예측기 \(g_\theta(x)\)의 파라미터 \(\theta\)를 결정하는 것을 예측기를 데이타에 fitting 한다고 부른다.
일반적으로 empirical risk \(\eloss(\theta)\)를 최소화하도록 예측기를 fiting하며, 이를 empirical risk minimization (ERM) 이라 부른다. 즉, ERM은 \(\eloss(\theta)\)를 최소화하는 \(\theta\)를 찾는 작업이다.
즉, ERM을 통해 주어진 데이타를 가장 잘 설명할 수 있는 \(\theta\)를 정할 수 있다.
선형 예측기 \(g_\theta(x)=\theta^T x\)의 경우는 아래와 같은 함수를 최소화하는 \(\theta\)를 고르는 문제로 표현할 수 있다.
일반적으로 임의의 empirical risk를 최소화하는 파라미터 \(\theta\)를 찾는 문제는 해석적으로 해결하기 어려우며 수치적인 최적화 numerical optimization 기법을 적용하여 해결한다.
Least squares linear regression#
예측기 파라미터 \(\theta \in \R^d\)를 갖는 선형 예측기 \(\hat y = g_\theta(x) = \theta^\tp x\)를 가정하자.
손실함수는 제곱 함수로 \(\loss(\hat y, y) = (\hat y - y)^2\) 정의하자.
그러면 empirical risk인 MSE는 아래와 같이 표현된다.
ERM 문제는 예측기의 MSE를 최소화하는 \(\theta\)를 찾는 문제가 되며, 이와 같은 문제를 linear least squares fitting 또는 linear regression 이라 부른다.
Least squares formulation#
MSE를 아래와 같이 행렬을 사용하여 표현해 보자.
여기서 행렬 \(X\in\R^{n \times d}\)와 벡터 \(y\in\R^n\)는 주어진 데이타 세트를 이용해 아래와 같이 정의된다.
ERM 문제는 least squares problem 표현됨을 확인할 수 있다. 즉, \(\|X \theta - y\|^2\)를 최소화하는 \(\theta\)를 찾음으로써 ERM 문제는 해결된다.
Least squares solution#
Least squares 문제는 주어진 \(X\)와 \(y\)에 대해 \(\norm{X\theta-y}^2\)를 최소화하는 \(\theta\)를 찾는 문제이다.
여기서 \(X \in\R^{n \times d}\)는 정사각형이거나 위아래로 긴 행렬이다 (\(d \leq n\)).
\(\norm{X\theta-y}^2\)는 최소화하기 위한 목적함수 objective function 라고 부른다.
\(X\)의 컬럼들이 linearly independent columns하다면 목적함수를 최소화하는 최적해 \(\theta\)는 아래와 같이 찾을 수 있다.
참고로, 실제로는 \(X^\dagger=(X^\tp X)^{-1}X^\tp\)를 직접적으로 계산하지는 않고 QR 분해 등의 효율적인 방법을 통해 최적해를 계산할 수 있다.
예를 들어, Python에서는
numpy의numpy.linalg.lstsq함수를 통해 위와 동일한 최적해를 매우 효율적인 방법으로 얻을 수 있다.
Numerical examples#
Polynomial fit#
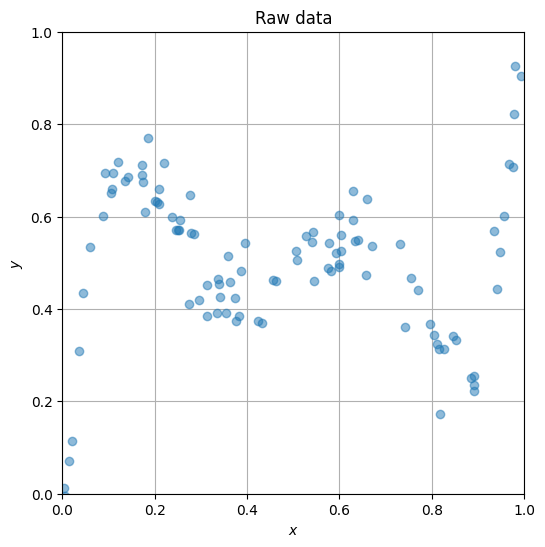
아래의 셀을 실행하면 실수 입력 데이타 \(x\)와 출력 데이타 \(y\)를 담고 있는 csv 파일을 로드한다. 이 데이타를 가지고 입력과 출력 사이의 관계를 찾아내 새로운 \(x\)가 들어오면 출력값을 예측할 수 있는 예측 모델을 만들려고 한다.
import numpy as np
import matplotlib.pyplot as plt
data = np.loadtxt('https://jonghank.github.io/ase3001/files/fit_data.csv', \
delimiter=',')
x, y = data[:,0], data[:,1]
plt.figure(figsize=(6,6), dpi=100)
plt.plot(x, y, 'o', alpha=0.5)
plt.grid()
plt.axis('square')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.title('Raw data')
plt.show()
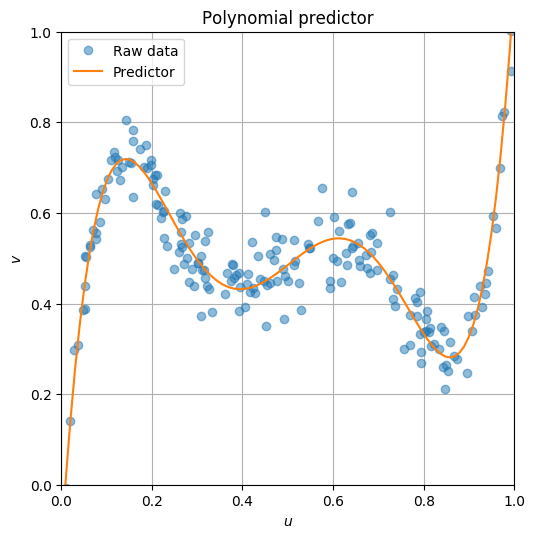
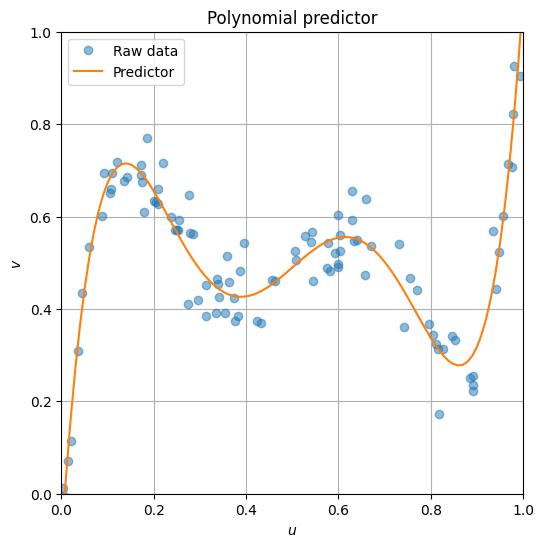
주어진 데이타 \(y\)를 \(x\)에 대한 5차 다항식 모델로 fitting하기로 한다.
모든 데이타에 대해 \(\hat{y}\)를 \({y}\)에 가깝도록 만드는 \(\theta = \bmat{\theta_0 & \cdots & \theta_5}^T\)를 찾으려고 하며, 이는 아래에 정의된 empirical risk를 최소화하는 \(\theta\)를 찾음으로써 해결된다.
여기서 행렬 \(X\)와 벡터 \(y\)는 아래와 같다.
n = len(x)
d = 6
X = np.zeros((n,d))
for i in range(d):
X[:,i] = x**i
theta_opt = np.linalg.lstsq(X, y, rcond=None)[0]
print(f'Optimal theta: {theta_opt}')
vp = np.linspace(0, 1, 100)
X_vp = np.zeros((len(vp),d))
for i in range(d):
X_vp[:,i] = vp**i;
plt.figure(figsize=(6,6), dpi=100)
plt.plot(x, y, 'o', alpha=0.5, label='Raw data')
plt.plot(vp, np.dot(X_vp, theta_opt), label='Predictor')
plt.grid()
plt.axis('square')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel(r'$u$')
plt.ylabel(r'$v$')
plt.title("Polynomial predictor")
plt.legend()
plt.show()
Optimal theta: [-1.08775601e-01 1.51579304e+01 -9.49190641e+01 2.39806312e+02
-2.64399727e+02 1.05545151e+02]
Diabete progression#
아래의 셀은 442명의 환자에 대한 의료 정보를 담고 있으며, 각각의 row가 환자 1명의 데이타를 의미한다. 왼쪽 열 개의 컬럼은 나티, 성별, BMI 등, 환자의 정보와 검사 기록 등을 포함하며, 가장 오른쪽 걸럼은 1년의 추적검사를 통해 확인된 해당 환자의 당뇨병 진행도를 의미한다.
import pandas as pd
df = pd.read_csv('https://jonghank.github.io/ase3001/files/diabetes_data.txt', delimiter='\t')
df
| AGE | SEX | BMI | BP | S1 | S2 | S3 | S4 | S5 | S6 | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 59 | 2 | 32.1 | 101.00 | 157 | 93.2 | 38.0 | 4.00 | 4.8598 | 87 | 151 |
| 1 | 48 | 1 | 21.6 | 87.00 | 183 | 103.2 | 70.0 | 3.00 | 3.8918 | 69 | 75 |
| 2 | 72 | 2 | 30.5 | 93.00 | 156 | 93.6 | 41.0 | 4.00 | 4.6728 | 85 | 141 |
| 3 | 24 | 1 | 25.3 | 84.00 | 198 | 131.4 | 40.0 | 5.00 | 4.8903 | 89 | 206 |
| 4 | 50 | 1 | 23.0 | 101.00 | 192 | 125.4 | 52.0 | 4.00 | 4.2905 | 80 | 135 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 437 | 60 | 2 | 28.2 | 112.00 | 185 | 113.8 | 42.0 | 4.00 | 4.9836 | 93 | 178 |
| 438 | 47 | 2 | 24.9 | 75.00 | 225 | 166.0 | 42.0 | 5.00 | 4.4427 | 102 | 104 |
| 439 | 60 | 2 | 24.9 | 99.67 | 162 | 106.6 | 43.0 | 3.77 | 4.1271 | 95 | 132 |
| 440 | 36 | 1 | 30.0 | 95.00 | 201 | 125.2 | 42.0 | 4.79 | 5.1299 | 85 | 220 |
| 441 | 36 | 1 | 19.6 | 71.00 | 250 | 133.2 | 97.0 | 3.00 | 4.5951 | 92 | 57 |
442 rows × 11 columns
주어진 10개의 입력 feature(와 1개의 constant feature)를 입력받아 1년 후의 당뇨병 진행도를 예측하는 선형 모델을 아래와 같이 설계할 수 있다.
Diabete progression, \(y\):
n, d = df.shape
X = np.hstack((np.ones((n,1)), df.values[:,:-1]))
y = df.values[:,-1]
theta_opt = np.linalg.lstsq(X, y, rcond=None)[0]
MSE = np.linalg.norm(X.dot(theta_opt)-y)**2/n
print(f'MSE: {MSE}')
print(f'RMSE: {np.sqrt(MSE)}')
MSE: 2859.6963475867506
RMSE: 53.476128764026576
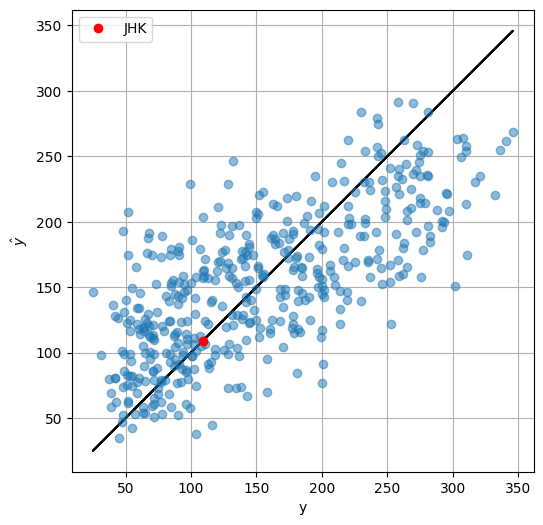
아래의 플롯은 설계된 예측기가 출력한 진행도와 실제 진행도를 비교한 것으로, diagonal 방향의 검정 실선에 놓인 데이타는 (\(\hat{y}=y\)) 예측 모델의 결과가 정확한 경우를 의미하고, 검정 실선과 먼 데이타는 예측 모델의 오차가 큰 경우를 의미한다.
plt.figure(figsize=(6,6), dpi=100)
plt.plot(y, y, 'k')
plt.plot(y, X.dot(theta_opt), 'o', alpha=0.5)
plt.xlabel('y')
plt.ylabel(r'$\hat{y}$')
plt.axis('square')
plt.grid()
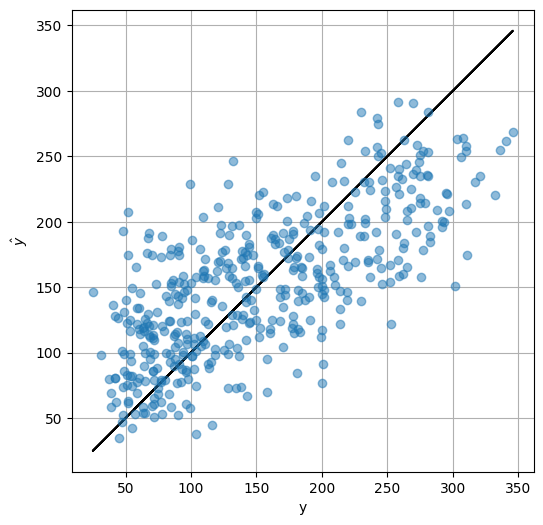
이제 이 모델을 활용하여 새로운 환자가 들어왔을 때 (\(X_\text{new}\)) 그 환자의 미래 1년간 당뇨병 진행도를 예측해 보자.Now suppose we got a new medical record from a new patient. 새 환자의 당뇨병 진행도는 \(\hat{y}_\text{new}=X_\text{new}\theta^*\)를 통해 쉽게 예측할 수 있으며, 이를 통해 대략적으로 이 환자가 당뇨병에 대하 얼마나 취약한지 예상할 수 있다.
# note that each feature represents
# u1: age
# u2: sex
# u3: bmi body mass index
# u4: map mean arterial pressure
# u5: s1 (tc) : total cholesterol
# u6: s2 (ldl): low density lipoprotein
# u7: s3 (hdl): high density lipoprotein
# u8: s4 (tch):
# u9: s5 (ltg):
# u10: s6 (glu):
# features: age sex bmi map tc ldl hdl tch ltg glu
X_JHK = np.array([41, 1, 18.3, 90, 171, 80.0, 74.9, 2, 4.75, 90.0])
X_JHK = np.hstack((1, X_JHK))
y_JHK = X_JHK.dot(theta_opt)
plt.figure(figsize=(6,6), dpi=100)
plt.plot(y, y, 'k')
plt.plot(y, X.dot(theta_opt), 'o', alpha=0.5)
plt.plot(y_JHK, y_JHK, 'ro', label='JHK')
plt.xlabel('y')
plt.ylabel(r'$\hat{y}$')
plt.legend()
plt.axis('square')
plt.grid()